Teaching modeling in introductory statistics

A comparison of formula and tidyverse syntaxes

Amelia McNamara @AmeliaMN

Pre-print

This talk is based on a paper I wrote, which is available as a pre-print via arXiv, https://arxiv.org/abs/2201.12960

Palmer Penguins

library(palmerpenguins)

Penguin data and penguin art by Allison Horst.

Summary statistics three ways

base

mean(penguins$body_mass_g[penguins$species == "Adelie"], na.rm = TRUE)
mean(penguins$body_mass_g[penguins$species == "Chinstrap"], na.rm = TRUE)
mean(penguins$body_mass_g[penguins$species == "Gentoo"], na.rm = TRUE)

tapply(penguins$body_mass_g, penguins$species, mean, na.rm = TRUE)

formula

mean(body_mass_g ~ species, data = penguins, na.rm = TRUE)

tidyverse

penguins %>%
  drop_na(body_mass_g) %>%
  group_by(species) %>%
  summarize(mean(body_mass_g))

Scatterplot three ways

base

plot(penguins$flipper_length_mm, penguins$bill_length_mm)

formula

gf_point(bill_length_mm ~ flipper_length_mm, data = penguins)

tidyverse

ggplot(penguins) +
  geom_point(aes(x = flipper_length_mm, y = bill_length_mm))

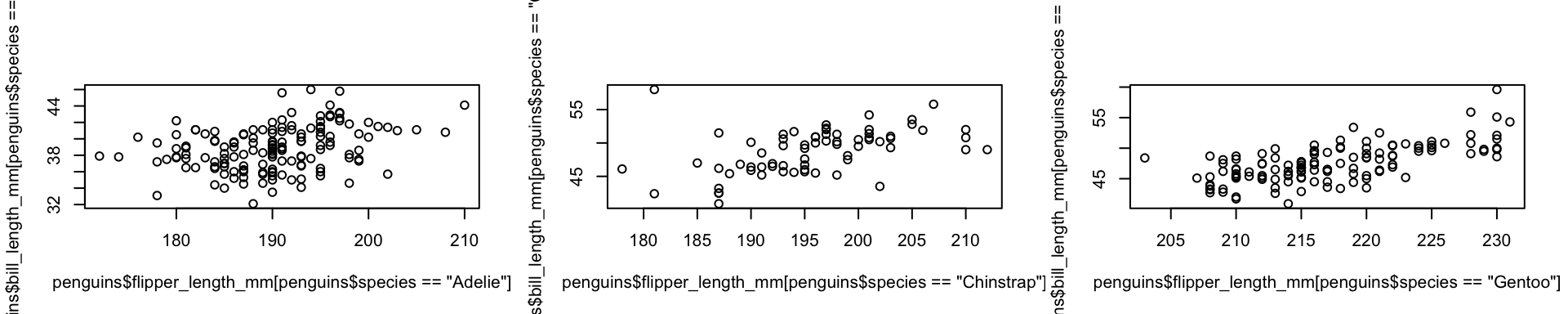
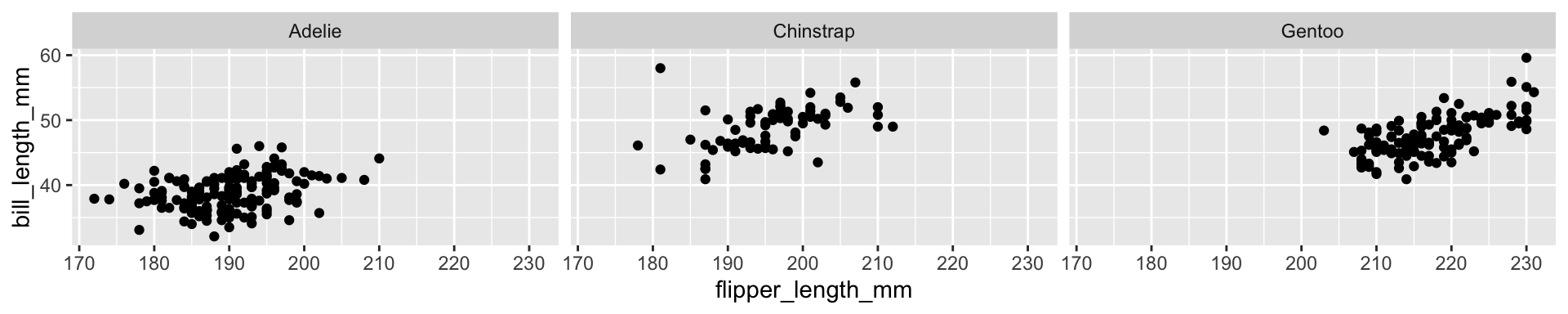
Sets of scatterplots three ways

base

par(mfrow = c(1, 3))
plot(penguins$flipper_length_mm[penguins$species == "Adelie"],
     penguins$bill_length_mm[penguins$species == "Adelie"])
plot(penguins$flipper_length_mm[penguins$species == "Chinstrap"],
     penguins$bill_length_mm[penguins$species == "Chinstrap"])
plot(penguins$flipper_length_mm[penguins$species == "Gentoo"],
     penguins$bill_length_mm[penguins$species == "Gentoo"])
# apply solution?

formula

gf_point(bill_length_mm ~ flipper_length_mm | species, data = penguins)

tidyverse

ggplot(penguins, aes(x = flipper_length_mm, y = bill_length_mm)) +
  geom_point() +
  facet_grid(~species)

Sets of scatterplots three ways

base

formula/tidyverse

Choosing syntax

There is debate in the statistics education community about which syntax is best to teach, particularly for the “first course.” All three syntaxes have their proponents, but the folks most interested in pedagogy tend to argue about whether formula or tidyverse is best.

• the base first philosophy typically comes from people who were taught base first, often using the man page for R. Jeff Leek has argued for the use of base graphics but very few arguments for base-first are grounded in pedagogy
• tidyverse first philosophy, as espoused by Mine Cetinkaya-Rundel, Jo Hardin, Ben Baumer, myself, Nick Horton, and Colin Rundel in An educator’s perspective on the tidyverse.
• formula first philosophy, “the third way”, as laid out by Nick Horton. This philosophy led to the mosaic package, which Horton coauthored with Randy Pruim and Danny Kaplan.

Head-to-head comparison

• Students enrolled in the same lecture class (60-90 students)
• Lecture was broken into three smaller sections for lab material
• I taught two of the sections (n=21 in each), and both were designated as using R
• Using random assignment (coin flip) I chose one to use tidyverse syntax and one to use formula syntax
• Similar students in both groups– mostly business majors, similar prior programming experience

Prior programming experience?.

	formula	tidyverse
No	10	9
Yes, but not with R	2	4

Why do this?

To get some data

Constraints breed creativity

Data

I was able to gather lots of data:

• RMarkdown documents and associated code
• Pre- and post-survey
• YouTube analytics
• RStudio Cloud analytics

getParseData()

The getParseData() function from utils allows you to parse R code and find all sorts of things about the parse tree. I just filtered for functions.

purled_labs <- list.files(path = here("data/prelabs"), full.names = TRUE)
names(purled_labs) <- list.files(path = here("data/prelabs"))
parsed_all <- map_dfr(purled_labs, ~getParseData(parse(file = .)), 
                      .id = "filename")
allfunctions <- parsed_all %>%
  filter(token == "SYMBOL_FUNCTION_CALL") 

Minimal reproducible… stats course

Like “Enough R for Intro Stats” by Randy Pruim.

The formula section saw a total of 37 functions and the tidyverse section saw 50, with an overlap of 18 functions between the two sections.

Neither of these numbers are very large!

The functions both sections of students saw included helper functions like library(), set.seed(), and set() (a function in the knitr options included in the top of each RMark- down document), statistics like mean(), sd(), and cor(), and modeling-related functions like aov(), lm(), summary() and predict().

What was hard? (formula edition)

Dealing with missing data.

options(na.rm = TRUE)
mean(body_mass_g ~ species, data = penguins, na.rm = TRUE)
cor(body_mass_g ~ species, data = penguins, use = "complete.obs")

Solutions:

• More consistency in prep.
• Teach some wrangling
• ??

What was hard? (tidyverse edition)

Explaining things with two categorical variables (two-way tables, inference)

penguins %>%
  group_by(sex, island) %>%
  summarize(n = n()) %>%
  mutate(prop = n / sum(n))

# A tibble: 4 × 4
# Groups:   sex [2]
  sex    island     n  prop
  <fct>  <fct>  <int> <dbl>
1 female Biscoe    80 0.567
2 female Dream     61 0.433
3 male   Biscoe    83 0.572
4 male   Dream     62 0.428

penguins %>%
  infer::prop_test(
    response = island,
    explanatory = sex,
    alternative = "two-sided",
    order = c("female", "male")
  )

# A tibble: 1 × 6
  statistic chisq_df p_value alternative lower_ci upper_ci
      <dbl>    <dbl>   <dbl> <chr>          <dbl>    <dbl>
1  1.78e-30        1    1.00 two.sided     -0.127    0.117

For comparison

mosaic::tally(island ~ sex, 
              data = penguins, 
              format = "proportion")

        sex
island      female      male
  Biscoe 0.5673759 0.5724138
  Dream  0.4326241 0.4275862

mosaic::prop.test(island ~ sex, 
                  data = penguins, 
                  success = "Biscoe")

    2-sample test for equality of proportions with continuity correction

data:  tally(island ~ sex)
X-squared = 2.8876e-30, df = 1, p-value = 1
alternative hypothesis: two.sided
95 percent confidence interval:
 -0.1248439  0.1147680
sample estimates:
   prop 1    prop 2 
0.5673759 0.5724138 

Pre- and post-survey

Not much difference between sections

Pre- and post-survey

Pre-lab length

RMarkdown documents, in lines

pre-lab videos, in minutes

Compute time

Model

Fit a linear mixed-effects, using month as a categorical variable. lme4 package doesn’t provide p-values, but we can look at confidence intervals.

Confidence intervals for coefficient estimates.

	2.5%	97.5%
.sig01	3.3	6.1
.sigma	4.5	5.9
(Intercept)	8.4	14.4
sectiontidyverse	-6.2	2.2
monthOctober	1.2	7.5
monthNovember	-4.9	1.5
monthDecember	-5.5	0.9
sectiontidyverse:monthOctober	0.4	9.4
sectiontidyverse:monthDecember	0.7	9.7

So, which should I use?

It depends!

I used formula this past semester when I taught the R labs again. Most students won’t go on to another stat class, and are mostly “users” of R rather than “doers.”

If most of my students were stat majors, I would definitely teach tidyverse. If it was intro data science, I would teach tidyverse.

My big suggestion is be consistent.

Constraints breed creativity!

Use getParseData() to learn how many functions you are using, and streamline.

Learn more

• Pre-print https://arxiv.org/abs/2201.12960
• Reproducible code to generate paper https://github.com/AmeliaMN/ComparingSyntaxForModeling
• Pre-lab documents and cheatsheets https://github.com/AmeliaMN/STAT220-labs

Thank you